如何用同一种下照灯均匀地打亮一个作业面

初醒悟

广州晓醒设计有限公司

摘 要：在办公、体育馆、展陈空间的照明设计案例中，有时希望用同一种下照灯均匀地打亮一个作业面。本文首先从理论上分析如何实现这个目标，再用数学工具求解它，最后给出一个算例。

引 言

数学，是一种强有力的工具，因为它可以“一劳永逸”地解决同一类问题。

照明设计中的分析计算离不开数学。利用好数学这个利器，不但会使照明设计更科学、更精准，而且可以让我们看清好多问题的本质，而非停留在表象上^[1]。

照度均匀度是指“规定表面上的最小照度与平均照度之比，符号是U₀”^[2]。照度均匀度是照明质量的重要指标之一。GB50034-2013《建筑照明设计标准》中，对于多数室内照明场所的照度均匀度U₀最低要求为0.6，精细操作的场所U₀最低要求为0.7。对于现有的常规灯具，U₀值达到0.8以上相当困难。

我们能做到用同一种下照灯均匀地打亮一个作业面么？目标是U₀值达到0.9以上。

本文配光曲线采用常规ies文件格式^{[3] [4]}。

1 分析

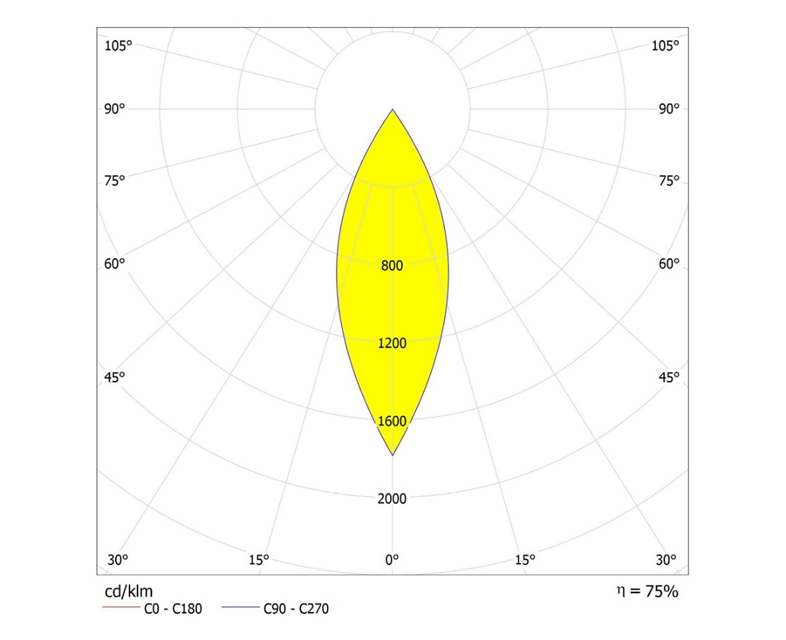
选用LED透镜加工简单、光输出效率高的轴对称式配光下照灯。此类灯具吸顶或吊装，会在水平作业面上打出圆形光斑。

为了提高水平照度均匀度，我们采用正三角形平面布灯方案，以确保所有灯具间的距离相等。如图1。

我们来研究其中的一个典型局部，计算模型如图2。每只灯正下方的照度最高，沿径向水平照度逐渐按照某种规律降低，至圆形光斑的边缘水平照度降至零。临近灯具的中心投影与圆形光斑的边沿重合。

我们知道，水平照度的计算公式为：

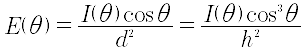
其中，I(θ)：光束方向与垂直方向之间夹角θ对应的光强；

d ：出光点与照度计算点间的距离；

h ：出光点与作业面的垂直高差。

距高比a = tanφ = AB/A’A，是一个重要参数。因为正是距高比，决定了函数的形状。

F是AB的中点；G是正三角形ABD的中心。

我们构造光强函数：

构成它的三个分量各有其不同的作用：

分子，既确保了灯具正下方（θ = 0˚），即圆形光斑的圆心处水平照度最高，又保证了光斑边缘（θ = φ）水平照度降至零；

分母，用来调节这条下降曲线的曲率；

系数k，在曲线形状已确定的前提下，用作调整光强比率。

将（2）式代入（1）式，我们得到：

于是，对于每一个a值，均有一个m值与之对应。亦即，有一种合适的配光曲线与之对应。

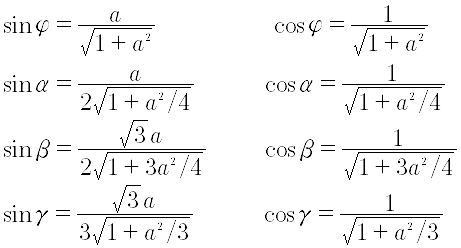
A点的水平照度：

F点的水平照度：

令以上二式相等，我们得到：

虽然通过上式很难推导出更简洁的m与a的关系式，但我们可以借助“Microsoft Mathematics”软件给出部分典型的数值解，见表1。

表1 部分典型距高比a对应的m数值

G点的水平照度：

表2 距高比a对应的E_G/E_A

2 算例

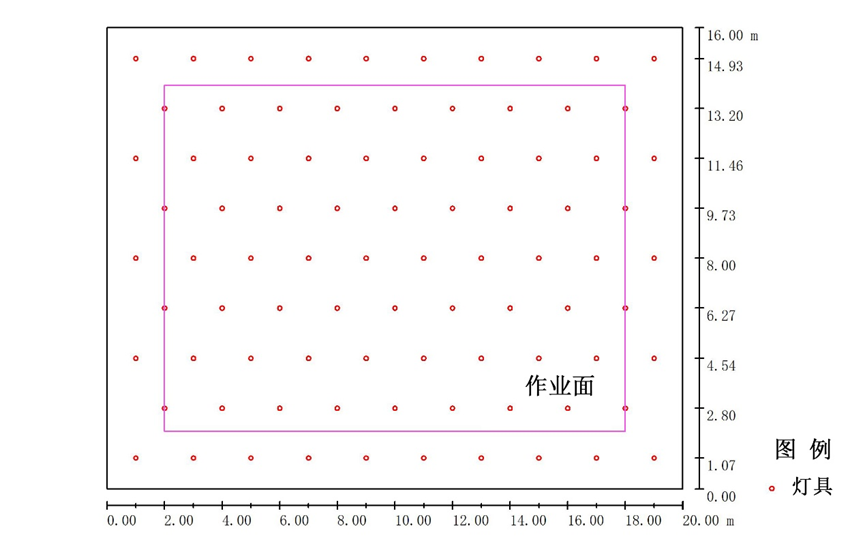
灯具吸顶安装，主要设计参数如表3：

表3 算例主要设计参数表

本算例对应的φ =34.992°，m = 2.483，k = 7780.0

故，a = 0.7对应的配光曲线光强函数：

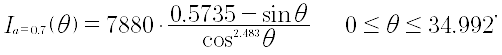
3 算例配光曲线文档

IESNA:LM-63-2002[TEST][TESTLAB][MANUFAC][LUMCAT][LUMINAIRE][LAMP] LED[BALLAST] N/A[ISSUEDATE][OTHER] B-Angle = 0.00 B-Tilt = 0.00TILT=NONE20 100.00 0.80 93 1 1 2 0.1500 0.1500 0.1501.0 1.0 20.000.00 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.0011.00 12.00 13.00 14.00 15.00 16.00 17.00 18.00 19.00 20.0021.00 22.00 23.00 24.00 25.00 26.00 27.00 28.00 29.00 30.0031.00 32.00 33.00 34.00 35.00 36.00 37.00 38.00 39.00 40.0041.00 42.00 43.00 44.00 45.00 46.00 47.00 48.00 49.00 50.0051.00 52.00 53.00 54.00 55.00 56.00 57.00 58.00 59.00 60.0061.00 62.00 63.00 64.00 65.00 66.00 67.00 68.00 69.00 70.0071.00 72.00 73.00 74.00 75.00 76.00 77.00 78.00 79.00 80.0081.00 82.00 83.00 84.00 85.00 86.00 87.00 88.00 89.00 90.00 90.50 180.000.004461.53704327.3936 4196.3634 4068.1927 3942.6355 3819.45193698.40773579.2727 3461.8204 3345.8264 3231.06803117.32273004.3675 2891.9776 2779.9257 2667.98072555.90642443.4605 2330.3933 2216.4461 2101.34991984.82371866.5728 1746.2868 1623.6378 1498.27761369.83551237.9153 1102.0924 961.9101 816.8754666.4553510.0711 347.0931 176.8344

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

4 灯具的适应性

针对某种距高比a设计的配光曲线，对于实际距高比在a附近的情形，照度均匀度U₀降低的程度如何？以下我们通过a值分别等于0.6、0.7、0.8对应的配光曲线，应用于a值在其附近的情形得出的照度均匀度U₀结果列表给出答案。

表4 三种配光曲线用于不同距高比情形下的U₀

a = 0.6与a = 0.8对应的配光曲线光强函数分别为：

5 结语

本文从理论上分析了用同一种下照灯均匀地打亮一个作业面的策略，以及此类灯具配光曲线光强函数的理论公式，给出的算例照度均匀度U₀最高可达0.975。后续实践可着手设计出对应于几种典型距高比的、多种不同功率规格的灯具，在需要高照度均匀度的场所加以运用，提升照明舒适度。

参 考 文 献

[1]初醒悟. 照明与数学[J]. 照明设计, 2012, 4: 78-79

.[2]《建筑照明设计标准》: GB50034-2013 [S], 2014. 4, 中国建筑工业出版社

[3]邹吉平. 灯具配光曲线及其标准格式[J]. 照明工程学报, 2007, 18(2): 76-80.

[4]钱群，宿天赋. 照明灯具光强分布曲线的格式解析与应用[J]. 照明工程学报. 2021,32(06): 57-63.